`linearsolvers`:¶

Contents¶

AMGCL

Files: callAMGCL - Invoke AMGCL Linear Solver Software

callAMGCL(A, b, varargin)¶

Invoke AMGCL Linear Solver Software

Description:

Solves the system of simultaneous linear equations

Ax = b

in which the coefficient matrix ‘A’ is sparse. Single right-hand side vector.

Synopsis:

 x              = callAMGCL(A, b)
 x              = callAMGCL(A, b, 'pn1', pv1, ...)

[x, err]        = callAMGCL(...)
[x, err, nIter] = callAMGCL(...)

Parameters:

A – Coefficient matrix.
b – System right-hand side vector.

Keyword Arguments:

isTransposed – Whether or not the coefficient matrix is transposed on
input. This simplifies converting MATLAB’s CSC matrix format to AMGCL’s CSR matrix input format. Default value: isTransposed = false.
- tolerance – Linear solver tolerance. Corresponds to parameter ‘solver.tol’ (relative residual reduction) of AMGCL. Default value: tolerance = 1.0e-6.
- maxIterations – Maximum number of linear iterations. Overrides ‘solver.maxiter’ if positive. Default value: maxIterations = 0 (use AMGCL solver’s default, typically 100).

Additional keyword arguments passed on to function getAMGCLMexStruct.

Returns:

x – Solution vector.
err – Norm of residual at end of solution process.
nIter – Number of linear iterations.

See also

mldivide, amgcl_matlab, getAMGCLMexStruct.

Contents¶

UTILS

Files: amgcl - Undocumented Utility Function amgcl_matlab - MEX-gateway to AMGCL Linear Solver Software amgcl_matlab_simple - MEX-gateway to AMGCL Linear Solver Software callAMGCL_cpr - Invoke AMGCL Linear Solver Software in CPR Mode getAMGCLDependencyPaths - Locate AMGCL Build Prerequisites on Current Computer System getAMGCLMexStruct - Undocumented Utility Function resetAMGCL - Undocumented Utility Function translateOptionsAMGCL - Translate AMGCL String Option Value to Integer Code

amgcl(mat, rhs, varargin)¶: Undocumented Utility Function

amgcl_matlab(varargin)¶

MEX-gateway to AMGCL Linear Solver Software

For more information about AMGCL, please see: Documentation: http://amgcl.readthedocs.io/en/latest/ GitHub repository: https://github.com/ddemidov/amgcl/tree/master/examples

Synopsis:

 x              = amgcl_matlab(A, b, amg_opt, tol, maxIter, id)

[x, err]        = amgcl_matlab(...)
[x, err, nIter] = amgcl_matlab(...)

Parameters:

A – Sparse coefficient matrix of system of simultaneous linear equations.
b – System right-hand side.
amg_opt – AMGCL options structure as defined by function getAMGCLMexStruct.
tol – Relative residual reduction tolerance. Positive scalar.
maxIter – Maximum number of linear iterations.
id – Solver method ID. Integer. Supported values are 1 for the regular solver and 2 for the CPR solver.

Returns:

x – Solution vector.
err – Norm of residual at end of solution process.
nIter – Number of linear iterations.

Note

For first-time use, this gateway will attempt to build a MEX-file using the configured C++ compiler. In order to do this, the paths to the dependencies AMGCL and BOOST can be specified via global variables, or the dependencies can be automatically downloaded by MRST if Internet access is available.

For instance, this can be done by executing the following: global BOOSTPATH AMGCLPATH % Define paths BOOSTPATH = ‘/path/to/boost’; AMGCLPATH = ‘/path/to/amgcl-repo’; % Build the binaries amgcl_matlab();

In addition, you will require a working C++ compiler (see mex -setup).

This gateway was last tested with commit

a551614040f0a7b793b41a4a63386675ca61d8da

of the AMGCL software (from GitHub: https://github.com/ddemidov/amgcl).

Linux (Ubuntu 18.04.2 LTS):

GCC 7.4.0 Boost 1.70.0
Linux (Mint 17.2):

GCC 4.9.4 Boost 1.63.0
MS Windows 10 (1809):

MSVC 19.16.27032.1 (Visual Studio 2017 15.9.15) Boost 1.70.0

See also

callAMGCL, getAMGCLMexStruct.

amgcl_matlab_simple(varargin)¶

MEX-gateway to AMGCL Linear Solver Software

For more information about AMGCL, please see: Documentation: http://amgcl.readthedocs.io/en/latest/ GitHub repository: https://github.com/ddemidov/amgcl/tree/master/examples

Synopsis:

 x              = amgcl_matlab(A, b, amg_opt, tol, maxIter, id)

[x, err]        = amgcl_matlab(...)
[x, err, nIter] = amgcl_matlab(...)

Parameters:

A – Sparse coefficient matrix of system of simultaneous linear equations.
b – System right-hand side.
amg_opt – AMGCL options structure as defined by function getAMGCLMexStruct.
tol – Relative residual reduction tolerance. Positive scalar.
maxIter – Maximum number of linear iterations.
id – Solver method ID. Integer. Supported values are 1 for the regular solver and 2 for the CPR solver.

Returns:

x – Solution vector.
err – Norm of residual at end of solution process.
nIter – Number of linear iterations.

Note

For first-time use, this gateway will attempt to build a MEX-file using the configured C++ compiler. In order to do this, the paths to the dependencies AMGCL and BOOST must be specified via global variables.

For instance, this can be done by executing the following: global BOOSTPATH AMGCLPATH % Define paths BOOSTPATH = ‘/path/to/boost’; AMGCLPATH = ‘/path/to/amgcl-repo’; % Build the binaries amgcl_matlab();

In addition, you will require a working C++ compiler (see mex -setup).

This gateway was last tested with commit

91348b025144b61a2d3b7417988373d0dc8c8d00

of the AMGCL software (from GitHub: https://github.com/ddemidov/amgcl).

Linux (Mint 17.2):

GCC 4.9.4 Boost 1.63.0
MS Windows 10 (1607):

MSVC 19.16.27024.1 (Visual Studio 15.9) Boost 1.68.0

See also

callAMGCL, getAMGCLMexStruct.

callAMGCL_cpr(A, b, block_size, varargin)¶

Invoke AMGCL Linear Solver Software in CPR Mode

Description:

Solves the system of simultaneous linear equations

Ax = b

in which the coefficient matrix ‘A’ is sparse. Single right-hand side vector.

Synopsis:

 x              = callAMGCL_cpr(A, b, block_size)
 x              = callAMGCL_cpr(A, b, block_size, 'pn1', pv1, ...)

[x, err]        = callAMGCL_cpr(...)
[x, err, nIter] = callAMGCL_cpr(...)

Parameters:

A – Coefficient matrix.
b – System right-hand side vector.
block_size – Size of sub-blocks. Positive integer.

Keyword Arguments:

isTransposed – Whether or not the coefficient matrix is transposed on
input. This simplifies converting MATLAB’s CSC matrix format to AMGCL’s CSR matrix input format. Default value: isTransposed = false.
- cellMajorOrder – Whether or not the coefficient matrix already is in cell-major ordering (i.e., whether or not the degrees of freedom are grouped by cell). If set, this makes the call into AMGCL proper less expensive than otherwise.
- tolerance – Linear solver tolerance. Corresponds to parameter ‘solver.tol’ (relative residual reduction) of AMGCL. Default value: tolerance = 1.0e-6.
- maxIterations – Maximum number of linear iterations. Overrides ‘solver.maxiter’ if positive. Default value: maxIterations = 0 (use AMGCL solver’s default, typically 100).

Additional keyword arguments passed on to function getAMGCLMexStruct.

Returns:

x – Solution vector.
err – Norm of residual at end of solution process.
nIter – Number of linear iterations.

getAMGCLDependencyPaths(varargin)¶

Locate AMGCL Build Prerequisites on Current Computer System

Synopsis:

[amgclpath, boostpath] = getAMGCLDependencyPaths
[amgclpath, boostpath] = getAMGCLDependencyPaths('pn1', pv1, ...)

Keyword Arguments:

amgcl_rev – Specific Git revision to download from AMGCL’s GitHub repository if necessary. Character vector. Default value:

amgcl_rev = ‘a551614040f0a7b793b41a4a63386675ca61d8da’.

Returns:

amgclpath – Location of AMGCL source code. Character vector.
boostpath – Location of Boost library headers. Character vector.

getAMGCLMexStruct(varargin)¶: Undocumented Utility Function

resetAMGCL(varargin)¶: Undocumented Utility Function

translateOptionsAMGCL(name, value)¶

Translate AMGCL String Option Value to Integer Code

Synopsis:

n = translateOptionsAMGCL(name, value)

Parameters:	name – Option name. Character vector. Must be one of ‘precondtioner’, ‘coarsening’, ‘relaxation’, or ‘solver’. value – Option value. String (character vector) pertaining to ‘name’.
Returns:	n – Integer option value known to underlying MEX gateway.

Examples¶

mrstModule add ad-core ad-blackoil spe10 blackoil-sequential mrst-gui linearsolvers

% Select layer 1
layers = 1;
mrstModule add ad-core ad-blackoil blackoil-sequential spe10

% The base case for the model is 2000 days. This can be reduced to make the
% problem faster to run.
T = 2000*day;
[state, model, schedule] = setupSPE10_AD('layers', layers, 'dt', 30*day, 'T',  T);

% Set up pressure and transport linear solvers
% AMGCL in AMG mode with default parameters
psolver = AMGCLSolverAD('coarsening', 'smoothed_aggregation', 'maxIterations', 50, 'tolerance', 1e-4, 'relaxation', 'ilu0');
psolver.keepNumber = model.G.cells.num;
% psolver.applyRightDiagonalScaling = true;
% AMGCL without AMG as a Krylov solver with ILU(0) preconditioner
tsolver = AMGCLSolverAD('preconditioner', 'relaxation', 'relaxation', 'ilu0', 'tolerance', 1e-4);

% Set up the sequential model
seqModel = getSequentialModelFromFI(model, ...
    'pressureLinearSolver', psolver,....
    'transportLinearSolver', tsolver);

% We set up a timestep selector that aims for timesteps where the
% maximum saturation change is equal to a fixed value.
stepSel = StateChangeTimeStepSelector(...
    'targetProps', {'s'},...
    'targetChangeAbs', 0.25);
% Run problem
solver = NonLinearSolver('timeStepSelector', stepSel);
[wsSeq, statesSeq, repSeq] = simulateScheduleAD(state, seqModel, schedule, 'NonLinearSolver', solver);

Solving timestep 01/75:                   -> 2 Hours, 2925 Seconds
Solving timestep 02/75: 2 Hours, 2925 Seconds -> 5 Hours, 2250 Seconds
Solving timestep 03/75: 5 Hours, 2250 Seconds -> 11 Hours, 900 Seconds
Solving timestep 04/75: 11 Hours, 900 Seconds -> 22 Hours, 1800 Seconds
Solving timestep 05/75: 22 Hours, 1800 Seconds -> 1 Day, 21 Hours
Solving timestep 06/75: 1 Day, 21 Hours   -> 3 Days, 18 Hours
Solving timestep 07/75: 3 Days, 18 Hours  -> 7 Days, 12 Hours
Solving timestep 08/75: 7 Days, 12 Hours  -> 15 Days
...

Example demonstrating different options for AMGCL¶

Generated from showOptionsAMGCL.m

Note that these choices mirror the names given in the AMGCL documentation: https://amgcl.readthedocs.io/en/latest/runtime.html

mrstModule add msrsb incomp coarsegrid spe10 linearsolvers

Setup problem¶

simple = false;
if simple
    % Create n by n grid
    n = 10;
    G = cartGrid([n, n, 1]);
    G = computeGeometry(G);
    rock = makeRock(G, 1, 1);
    W = [];
    W = addWell(W, G, rock, 1, 'type', 'rate', 'val', 1);
    W = addWell(W, G, rock, G.cells.num, 'type', 'bhp', 'val', 0);
else
    % Take part of SPE10 benchmark
    layers = 1;
    [G, W, rock] = getSPE10setup(layers);
end
% Set up linear system by calling the incompTPFA solver without a linear
% solver
fluid = initSingleFluid('rho', 0, 'mu', 1);
state = initResSol(G, 0);
state = incompTPFA(state, G, computeTrans(G, rock), fluid, 'Wells', W, 'matrixOutput', true, 'LinSolve', @(A, b) 0*b);
A = state.A;
b = state.rhs;
% Reduce to only wells
[A, b] = eliminateWellEquations(A, b, G.cells.num);

makeChoice = @(text, choices)  listdlg('PromptString',  text,...
                                       'SelectionMode', 'single',...
                                       'ListString',    choices);

Warning: Inconsistent Number of Phases.  Using 1 Phase (=min([3, 1, 1])).

Select preconditioner¶

There are two options here. If relaxation is chosen, AMG will be used as a preconditioner. If relaxation is chosen, no multigrid will be used and the solver will be a simpler Krylov solver with relaxation as a preconditioner. The coarsening option chosen later in this example will not be used in this case.

preconditioners = {'amg', ...
                   'relaxation'};
index = makeChoice('Select solver', preconditioners);
precond = preconditioners{index};

Select solver¶

Choices for Krylov acceleration

solvers = {'bicgstab', ...
% Biconjugate gradient stabilized method
           'cg', ...
% Conjugate gradient
           'bicgstabl', ...
% Bicgstab variant
           'gmres', ...
% Generalized minimal residual method
           'lgmres', ...
% GMRES variant
           'fmgres', ...
% Flexible-GMRES
           'idrs'}; % Induced Dimension Reduction method IDR(s)
index = makeChoice('Select Krylov-solver', solvers);
solver = solvers{index};

Select coarsening and interpolation scheme for AMG¶

coarsening = {'ruge_stuben', ...
% Ruge-stuben coarsening ("standard" coarsening)
              'smoothed_aggregation', ...
% Aggregation with smoothed iterates
              'aggregation', ...
% Aggregation - very fast coarsening due to very simple constant interpolation
              'smoothed_aggr_emin'}; % Aggregation with energy-minimizing smoothing
index = makeChoice('Select coarsening', coarsening);
coarsen = coarsening{index};

Select relaxation (“smoother”)¶

relaxations = {'spai0', ...
% Sparse approximate inverse, degree 0
               'spai1', ...
% Sparse approximate inverse
               'gauss_seidel', ...
% Gauss-seidel
               'ilu0', ...
% Incomplete LU-factorization without fill-in
               'iluk', ...
% Level-based ILU
               'ilut', ...
% Thresholded ILU
               'damped_jacobi', ...
% Damped Jacobi
               'chebyshev'}; % Chebyshev smoothing
index = makeChoice('Select relaxation', relaxations);
relax = relaxations{index};

Solve the system¶

tic();
[x, err, iter] = callAMGCL(A, b, ...
                    'coarsening', coarsen,...
                    'relaxation', relax, ...
                    'solver', solver, ...
                    'maxIterations', 100, ...
                    'preconditioner', precond, ...
                    'verbose', true);
t_amg = toc();
fprintf('%d iterations done in %f seconds. Final residual: %e\n', iter, t_amg, err);

AMGCL solver recieved problem with 13200 degrees of freedom. System has block size of 0.
Solving with 8 threads using OpenMP.
Initializing solver...
Solver setup took 0.013 seconds.
Solver
======
Type:             BiCGStab
Unknowns:         13200
...

Additional options¶

There are many additional options which can be set through the AMGCL struct. Generally, these can be passed as keyword arguments to callAMGCL and other routines which rely on AMGCL. Especially interesting options are - ncycle (number of multigrid cycles) - npre (number of presmootings) - npost (number of postsmoothings) As well as options relating to the coarsening hierarchy: - rs_eps_strong (strong threshold, ruge_stuben) - aggr_eps_strong (strong threshold, aggregation)

str = getAMGCLMexStruct();

disp(str)

preconditioner: 1
                 coarsening: 3
                 relaxation: 1
               s_relaxation: 3
                     solver: 4
                 block_size: 0
                active_rows: 0
                    use_drs: 0
...

Example demonstrating AMGCL on a few test problems¶

Generated from testAMGCL.m

mrstModule add msrsb incomp coarsegrid spe10 linearsolvers

Setup problem¶

simple = false;
if simple
    % Create n by n grid
    n = 10;
    G = cartGrid([n, n, 1]);
    G = computeGeometry(G);
    rock = makeRock(G, 1, 1);
    W = [];
    W = addWell(W, G, rock, 1, 'type', 'rate', 'val', 1);
    W = addWell(W, G, rock, G.cells.num, 'type', 'bhp', 'val', 0);
else
    % Take part of SPE10 benchmark
    layers = 1:5;
    [G, W, rock] = getSPE10setup(layers);
end
% Set up linear system by calling the incompTPFA solver without a linear
% solver
fluid = initSingleFluid('rho', 0, 'mu', 1);
state = initResSol(G, 0);
state = incompTPFA(state, G, computeTrans(G, rock), fluid, 'Wells', W, 'matrixOutput', true, 'LinSolve', @(A, b) 0*b);
A = state.A;
b = state.rhs;
% Reduce to only wells
[A, b] = eliminateWellEquations(A, b, G.cells.num);

Compare with AGMG (if available)¶

try
    mrstModule add agmg
    tic();
    x_agmg = agmg(A, b, [], [], [], true);
    t_agmg = toc();
catch
    x_agmg = nan*b;
    t_agmg = nan;
end

No module mapping found for
  * agmg

Call AMGCL in AMG mode¶

tic();
x = callAMGCL(A, b, 'coarsening', 'ruge_stuben',...
                    'relaxation', 'spai0', ...
                    'preconditioner', 'amg', 'verbose', true);
t_amg = toc();

AMGCL solver recieved problem with 66000 degrees of freedom. System has block size of 0.
Solving with 8 threads using OpenMP.
Initializing solver...
Solver setup took 0.089 seconds.
Solver
======
Type:             GMRES(30)
Unknowns:         66000
...

Call AMGCL in preconditioner mode¶

tic();
x = callAMGCL(A, b, 'relaxation', 'ilu0',...
                    'maxIterations', 1000, ...
                    'preconditioner', 'relaxation', 'verbose', true);
t_relax = toc();

AMGCL solver recieved problem with 66000 degrees of freedom. System has block size of 0.
Solving with 8 threads using OpenMP.
Initializing solver...
Solver setup took 0.017 seconds.
Solver
======
Type:             GMRES(30)
Unknowns:         66000
...

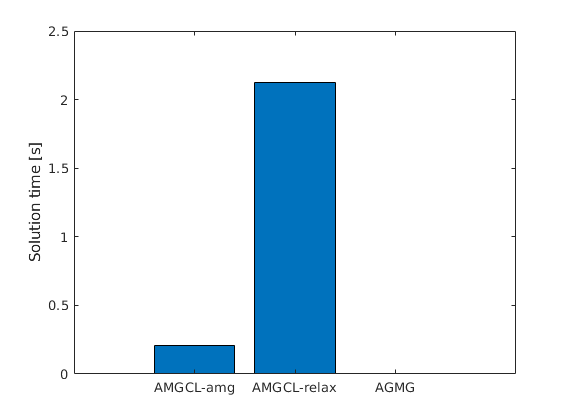
Plot time taken¶

clf;
bar([t_amg, t_relax, t_agmg])
set(gca, 'XTicklabel', {'AMGCL-amg', 'AMGCL-relax' 'AGMG'});
ylabel('Solution time [s]');

Example demonstrating AMGCL on a few test problems¶

Generated from testAMGCL_cpr.m

mrstModule add msrsb incomp coarsegrid spe10 linearsolvers ad-core ad-blackoil ad-props

Setup problem¶

testcase = 'spe10';
switch lower(testcase)
    case 'simple'
        nx = 10;
        ny = nx;
        G = cartGrid([nx, ny, 1], [1, 1, 1]);
        G = computeGeometry(G);

        rock = makeRock(G, 0.1*darcy, 0.5);

        fluid = initSimpleADIFluid('c', [1, 1, 1]*1e-5/barsa);
        model = TwoPhaseOilWaterModel(G, rock, fluid);

        state0 = initResSol(G, 100*barsa, [0.5, 0.5]);

        bc = [];
        src = [];
        W = [];

        bc = pside(bc, G, 'xmin', 50*barsa, 'sat', [1, 0]);
        bc = pside(bc, G, 'xmax', 50*barsa, 'sat', [1, 0]);

        forces = struct('bc', bc, 'W', W, 'src', src);
        dt = 30*day;
    case 'spe10'
        mrstModule add spe10
        [state0, model, schedule]  = setupSPE10_AD('layers', 1);
        forces = schedule.control(1);
        dt = schedule.step.val(1);
        G = model.G;
    case 'spe9'
        [G, rock, fluid, deck, state0] = setupSPE9();
        model = selectModelFromDeck(G, rock, fluid, deck);
        schedule = convertDeckScheduleToMRST(model, deck);
        forces = schedule.control(1);
        dt = schedule.step.val(1);
end
% Set up model to get a linearized system
model = model.validateModel(forces);
state0 = model.validateState(state0);
% Get equations for time-step
state = state0;
problem = model.getEquations(state0, state, dt, forces, 'iteration', inf);
[A0, b0] = problem.getLinearSystem();
% Use linear solver class to perform schur complement and remove wells from
% system
ncomp = model.water + model.oil + model.gas;
lsolve = BackslashSolverAD();
lsolve.keepNumber = ncomp*G.cells.num;
[A0, b0, sys] = lsolve.reduceLinearSystem(A0, b0);

% Make a simple pressure equation via an unweighted sum of the equations.
% In general, this is not always accurate. The AMGCL_CPRSolverAD solver
% class has implemented more sophisticated variants (e.g. dynamic row-sum,
% true-impes, quasi-impes, etc) which are used later in this example.
pix = 1:G.cells.num;
for i = 2:ncomp
    ix = (1:G.cells.num) + (i-1)*G.cells.num;
    A0(pix, :) = A0(pix, :) + A0(ix, :);
    b0(pix) = b0(pix) + b0(ix);
end
% Reorder to cell-major format (required by solver). MRST uses
% equation-major ordering by default.
subs = getCellMajorReordering(G.cells.num, ncomp);

b0 = b0./norm(b0, inf);
A = A0(subs, subs);
b = b0(subs);
% b = b0;
its = 100;
% AMGCL/C++ uses cell-major ordering, we do this outside to get more
% reliable timing results.
At = A';

mrstVerbose on

Call solver¶

tic();
x1 = callAMGCL_cpr(At, b, ncomp, 'isTransposed', true, 'maxIterations', its, 'cellMajorOrder', true);
t_wrapper = toc();

AMGCL solver converged to 7.663184e-07 in 17 iterations after 0.05 seconds.

Setup SPE9 black-oil case¶

[G, rock, fluid, deck, state] = setupSPE9();
model = selectModelFromDeck(G, rock, fluid, deck);
model.AutoDiffBackend = DiagonalAutoDiffBackend('useMex', true);
schedule = convertDeckScheduleToMRST(model, deck);

No converter needed in section 'REGIONS'.
No converter needed in section 'SUMMARY'.
Adding 1200 artificial cells at top/bottom

Processing regular i-faces
 Found 10625 new regular faces
Elapsed time is 0.009716 seconds.

...

Solve the schedule with AMGCL-CPR as the linear solver¶

lsolve = AMGCL_CPRSolverAD('maxIterations', 200, 'tolerance', 1e-3);
lsolve.setSRelaxation('ilu0');
% We can set coarsening and solver options as well
lsolve.setCoarsening('aggregation');
lsolve.setSolver('bicgstab');
[wellSols, states, report] = simulateScheduleAD(state, model, schedule, 'linearsolver', lsolve);

*****************************************************************
********** Starting simulation:    35 steps,   900 days *********
*****************************************************************
Preparing model for simulation...
Model ready for simulation...
Preparing schedule for simulation...
Schedule ready for simulation...
Validating initial state...
...

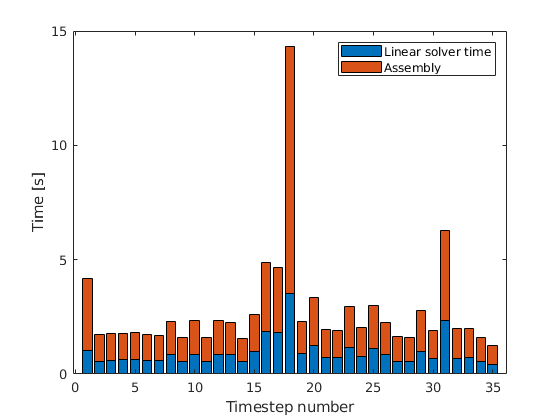
Plot breakdown of simulator time vs linear solver time¶

nstep = numel(report.ControlstepReports);
ls_time = zeros(nstep, 1);
for i = 1:nstep
    rr = report.ControlstepReports{i};
    for j = 1:numel(rr.StepReports{1}.NonlinearReport)
        rrr = rr.StepReports{1}.NonlinearReport{j};
        if rrr.Converged
            continue
        end
        if isfield(rrr.LinearSolver, 'SolverTime')
            ls_time(i) = ls_time(i) + rrr.LinearSolver.SolverTime;
        end
    end
end
% Plot per-step breakdown
figure;
bar([ls_time, report.SimulationTime - ls_time], 'stacked')
legend('Linear solver time', 'Assembly');
xlabel('Timestep number');
ylabel('Time [s]');

linearsolvers:¶

Examples¶

Example demonstrating different options for AMGCL¶

Setup problem¶

Select preconditioner¶

Select solver¶

Select coarsening and interpolation scheme for AMG¶

Select relaxation (“smoother”)¶

Solve the system¶

Additional options¶

Example demonstrating AMGCL on a few test problems¶

Setup problem¶

Compare with AGMG (if available)¶

Call AMGCL in AMG mode¶

Call AMGCL in preconditioner mode¶

Plot time taken¶

Example demonstrating AMGCL on a few test problems¶

Setup problem¶

Call solver¶

Setup SPE9 black-oil case¶

Solve the schedule with AMGCL-CPR as the linear solver¶

Plot breakdown of simulator time vs linear solver time¶

`linearsolvers`:¶